Оптово-торговым и транспортным кампаниям

Наша команда специалистов разработает для Вас систему автоматического формирования оптимального маршрута доставки продукции на точки розницы. Оптимальные пути будут разработаны с помощью метода Кларка-Райта.

 

Метод Кларка-Райта был разработан двумя британскими учеными Г. Кларком (G. Clarke) и Дж.В. Райтом (J.W. Right). Несмотря на давность разработки (метод опубликован в 1963 г.), он до сих пор остается самым популярным методом для решения данной задачи, о чем свидетельствует практика его применения.

Метод Кларка-Райта относится к числу приближенных, итерационных методов и  предназначается для компьютерного решения задачи развозки. Погрешность решения не превосходит в среднем 5-10%. Достоинствами метода являются его простота, надежность и гибкость, что позволяет учитывать целый ряд дополнительных факторов, влияющих на конечное решение задачи.

Рассмотрим метод Кларка-Райта на примере. За основу возьмем исходные данные из таблицы 1.

Таблица 1. Исходные данные

где x_i, y_i – координаты i—го получателя, q_i – объем спроса i—го получателя, шт.

 

Местоположение оптовой базы и 12 получателей, а также объем поставок каждому получателю приведены на рисунке 1.

На этом же рисунке указана и исходная схема развозки грузов. Согласно исходной схеме, для доставки груза каждому отдельному получателю организуется отдельный маршрут. Например, водитель загружает в кузов партию 450 шт. и везет ее в пункт 1, там разгружается, затем возвращается на базу, берет вторую партию 400 шт. и везет ее в пункт 2 и т.д. Таким образом, исходная схема развозки включает в себя только радиальные маршруты движения автомобиля, причем количество радиальных маршрутов совпадает с количеством получателей. В данном случае, схема развозки состоит из 12 радиальных маршрутов.

Суть метода заключается в том, чтобы, отталкиваясь от исходной схемы развозки, по шагам перейти к оптимальной схеме развозки с кольцевыми маршрутами. С этой целью вводится такое понятие, как километровый выигрыш. 

 

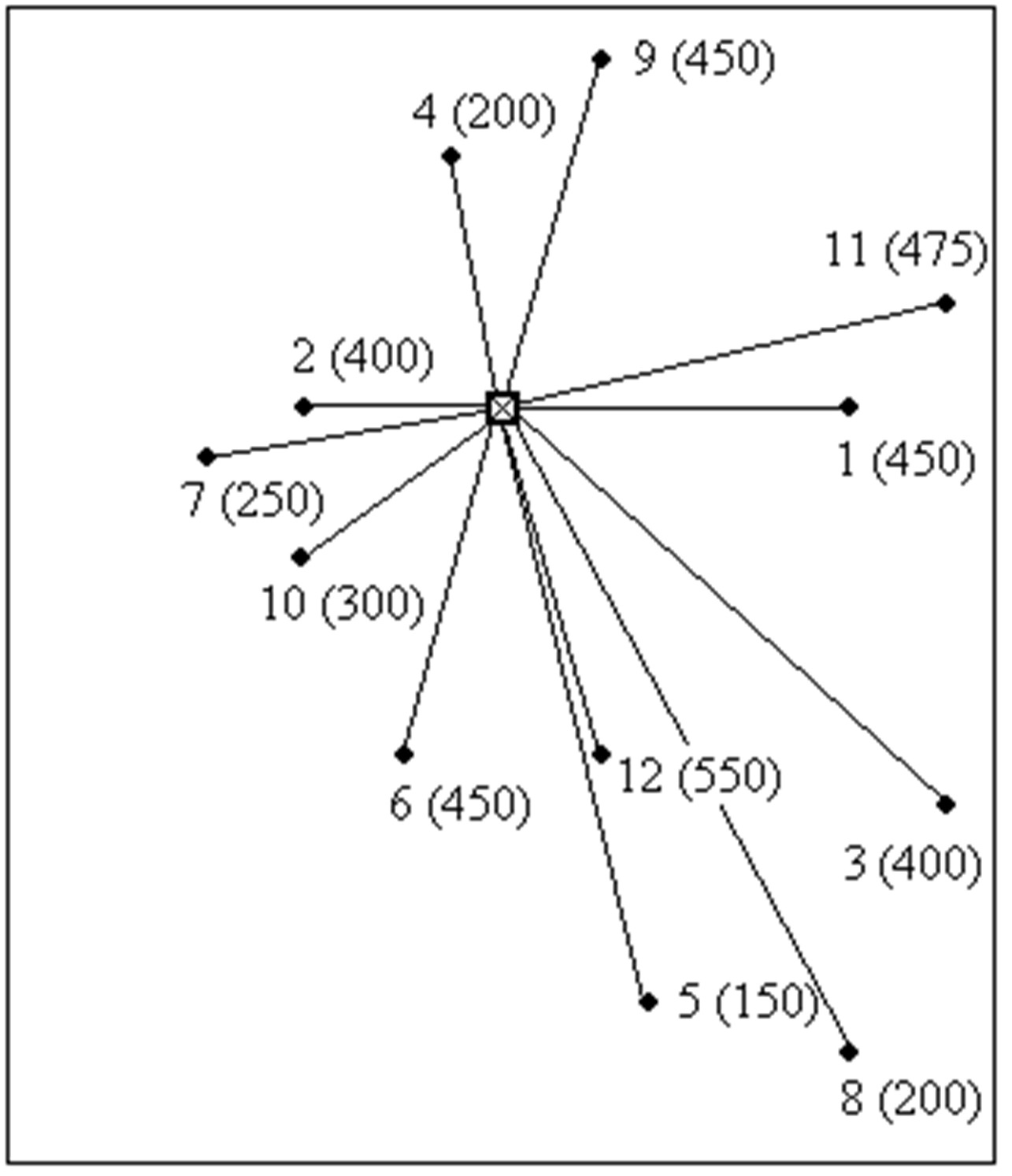
   Рисунок 1.

 

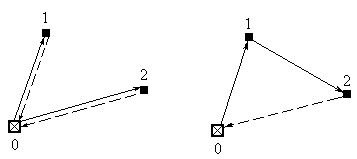
Рисунок 2.

 

На рисунке 2 отображены две схемы развозки. Схема развозки А (слева) обеспечивает доставку грузов в пункты 1 и 2 по радиальным маршрутам. Схема развозки B предполагает доставку грузов в пункты 1 и 2 по кольцевому маршруту. 

Используя Метод Кларка-Райта суммарный километровый выигрыш составляет:

S = 23,0 + 21,4 + 14,6 + 13,4 + 8,8 + 8,3 + 7,9 + 7,8 = 105,3 км

а общий пробег автотранспорта, соответственно:

L₁ = L₀ – S = 195 –105,3 = 89,7 км

Графически оптимальная схема развозки представлена на рисунке 3. Как видно, оптимальная схема развозки включает в себя четыре кольцевых маршрута (вместо первоначальных 12 радиальных маршрутов). Результаты расчетов сведены в таблицу 2:

 

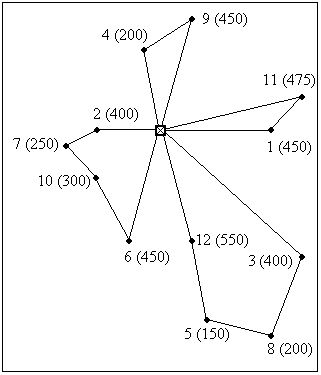
Рисунок 3.

 

Таблица 2

Результат решения задачи развозки

 

Заказать разработку.